- 선형 탐색(순차 탐색)의 O(n)를 O(logn)으로 줄여줌
- sort 함수로 정렬을 먼저 시행한 후에, 이분 탐색
- sort()가 arr와 vec 둘 다 가능한 것처럼
binary_search(), lower_bound(), upper_bound() 모두 arr와 vec 둘 다 가능
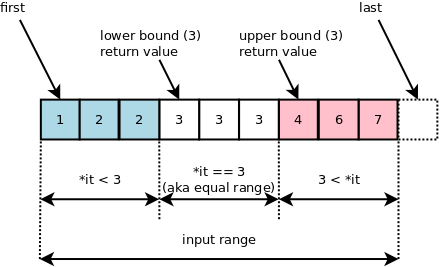
- 아래와 같이 초기화했다고 가정하겠다.
int arr[] = { 4, 12, 11, 10, 4, 2, 4, 5, 14, 1 };
int N = sizeof(arr) / sizeof(int);
sort(arr, arr + N);- 정렬 후에의 원소 구성은 다음과 같다.
1 2 4 4 4 5 10 11 12 14
원소 1개를 찾을 때
1) 존재 유무를 찾을 때
cout << binary_search(arr, arr + N, 3) << endl; // 3은 없으므로 0 출력
cout << binary_search(arr, arr + N, 4) << endl; // 4는 있으므로 1 출력2) 인덱스를 찾을 때
cout << lower_bound(arr, arr + N, 1) - arr << endl; // 1이 있는 위치는 0번째이므로 0출력
cout << lower_bound(arr, arr + N, 12) - arr << endl; // 12가 있는 위치는 8번째이므로 8출력
원소 여러 개를 찾을 때
1) 개수를 찾을 때
cout << upper_bound(arr, arr + N, 4) - lower_bound(arr, arr + N, 4) << endl; // 4는 3개이므로 3출력2) 인덱스를 찾을 때
int begin = lower_bound(arr, arr + N, 4) - arr; // '4의 인덱스들 중 가장 값은 값'이므로 2
int end = upper_bound(arr, arr + N, 4) - arr; // '4의 인덱스들 중 가장 큰 값 + 1'이므로 5
while (begin != end) {
cout << begin << " "; // 2 3 4 출력
begin++;
}
내림차순일 때
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int arr[] = { 4, 12, 11, 10, 4, 2, 4, 5, 14, 1 };
int N = sizeof(arr) / sizeof(int);
sort(arr, arr + N, greater<int>());
for (int i = 0; i < N; i++) {
cout << arr[i] << " ";
}
cout << endl;
cout << binary_search(arr, arr + N, 3, greater<int>()) << endl;
cout << binary_search(arr, arr + N, 4, greater<int>()) << endl;
cout << lower_bound(arr, arr + N, 1, greater<int>()) - arr << endl;
cout << lower_bound(arr, arr + N, 12, greater<int>()) - arr << endl;
cout << upper_bound(arr, arr + N, 4, greater<int>()) - lower_bound(arr, arr + N, 4, greater<int>()) << endl;
int begin = lower_bound(arr, arr + N, 4, greater<int>()) - arr;
int end = upper_bound(arr, arr + N, 4, greater<int>()) - arr;
while (begin != end) {
cout << begin << " ";
begin++;
}
return 0;
}
* 참고
찾고자하는 값이 없을 때 lower_bound와 upper_bound의 리턴값은?
- (위 예시의 경우) arr의 크기가 10이므로, 0 또는 10 중 하나 리턴
- 비교 함수의 종류와 찾고자 하는 값에 따라 결과가 다름
- 따라서 사용하지 않는 것이 안전
'알고리즘 > 이분탐색' 카테고리의 다른 글
| 백준 1654번 : 랜선 자르기 (0) | 2021.01.21 |
|---|---|
| 백준 2805번 : 나무 자르기 (0) | 2021.01.17 |
| 백준 1920번 : 수 찾기 (0) | 2021.01.16 |
| 백준 10815번 : 숫자 카드 (0) | 2020.12.31 |